Drag and solar radiation

Since ERS-1 encircles the earth at a relatively low altitude of 780 km and has a comparatively large cross-sectional area, the orbit is affected considerably by atmospheric drag [Kuijper, 1991]. Especially when the more recent gravity models are applied, drag mismodelling is a major error source in the orbit determination. The atmospheric drag is dependent on the atmospheric density, which varies significantly along the orbit, because of changes in the satellite's altitude and geomagnetic influences, but also from day to day, depending mainly on the solar activity. In the orbit computations these effects are covered by the DTM atmospheric model. To quantify the solar activity, daily measured or predicted 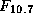and 3-hourly 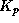values are input to the model.

Both atmospheric drag and solar radiation pressure act upon a large satellite with a complex shape, of which the attitude varies along the orbit. In the surface forces analysis the satellite's complex shape is modelled by 10 panels: 6 panels make up the body of the spacecraft and 4 panels model the front and back of the SAR antenna and solar array. To compute the drag, the effective cross-sectional area A is determined, based on the area and orientation of the panels with respect to the satellite's velocity vector. This orientation may vary in time due to the satellite's attitude control strategy and pointing of the solar array. The solar radiation force also takes into account the reflection, absorption, and emission properties of each panel.

Finally, the atmospheric drag is determined on the basis of the formula,

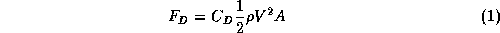
where V is velocity and 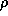is the atmospheric density. Theoretically, the drag coefficient 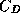is around 2.3. Because of imperfections in the modelling of the surface forces a series of 12-hourly drag coefficients are estimated per arc.

Similarly, the solar radiation force is given by

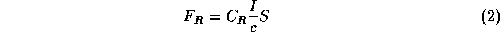
where I is the radiation intensity, c is the velocity of light, and S is the cross-sectional area perpendicular to the direction of the solar rays. The solar radiation coefficient 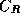is fixed to the theoretical value of 1.0 in the orbit computations.